二叉堆与堆排序要点

Posted on In

二叉堆，堆排序，与优先队列要点

今天看完了红皮《算法》第二章的优先队列那一节。二叉堆，堆排序，优先队列，这些都是难舍难分密切相关的几个概念。一句话来说，优先队列作为一种高效的数据结构，其实现依赖于二叉堆这么一种数据结构。借助于优先队列，能实现一种时间复杂度为logn的原地排序算法，堆排序。

要点：

  1. 二叉堆定义（用数组表示时的细节）
  2. 插入（尾端叶子节点）与删除（根节点）的过程
  3. 建堆方式 + sink 下沉操作 = 堆排序——堆排序的过程
  4. 堆排序的优点与缺点
    1. 优点：内存使用，原地排序
    2. 缺点：CPU cache 缓存命中，非稳定排序，比较次数大于快排
  5. 复杂度得出过程

[TOC]

二叉堆定义与数组表示

根节点大于等于左右两个子节点。当储存为数组时，根节点放在索引 1 的位置，为了计算便利数组的索引零不存储数据。位置为 k 的节点的父节点位置是 p <= k/2，子节点在数组中的位置是 2k 和 2k+1。如图：

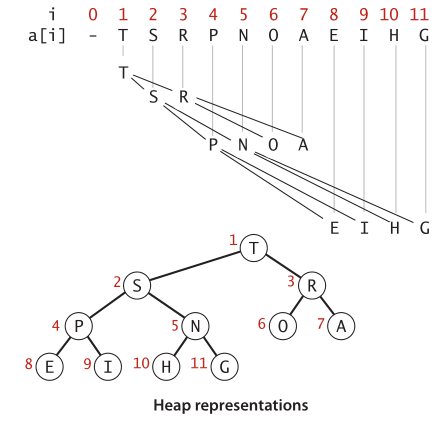
Heap Representations

另外，二叉堆属于完全二叉树。

二叉堆删除最大节点与插入数据过程

上浮、下沉操作

这两个操作是插入、删除 API 的基础操作。

上浮 swim 是指当某节点的子节点大于其父节点，破坏了堆的有序性，则将这个过大的子节点与它的父节点交换。如果交换之后，该子节点仍然大于交换位置之后的父节点，继续交换。这个过程就被形象化称为上浮。最终，节点上浮到正确的位置，它的父节点大于它，所有子节点小于它。每上浮一次需要 1 次比较。

下沉 sink 是相反的操作，由上至下比较。如果某节点小于它的子节点，则发生交换。每次下沉需要两次比较。首先比较找出两个子节点中较大的那个，然后比较较大子节点与父节点，如果父节点小于则交换。

删除最大/根节点

在大端二叉堆中，根节点就是堆中最大元素。将根节点删除/取出之后，把堆中最末尾的元素（也就是树中最大一层最右边的叶子节点）放在根节点的位置，然后对这个节点进行下沉操作。

每次删除操作，需要的时间复杂度最坏为 $\log n$，也就是从根节点一直比较、交换到叶子节点。假设树高度为 h，最坏情况下需要 h 次交换，2h 次比较。与此同时，作为一颗完全二叉树，二叉堆的高度 h 始终小于等于 $\log$2$n$，也就是 $\logn$ 复杂度。

插入数据

插入的数据将被放在最末端/最右端的叶子节点，然后对其使用上浮操作。最坏情况下需要 h 次比较，h 次交换，所以复杂度也为 $\log n$。

堆排序对数据的初始化：建堆

优先队列实现注意小细节

  1. sink 的调用条件是当前被下沉节点的子节点索引小于等于优先队列元素数量。否则，在边界条件时，就会导致有元素没有被下沉。举个例子，当队列还有三个元素，star, was, worst， 删除顶端元素之后在顶端插入末尾元素 worst，此时 worst 子节点为 was，索引为 1*2 = 2，大于等于优先队列的元素总数量，sink 操作没有调用，worst 元素先于 was 被取出队列。

  2. 在下沉 sink 操作时，在将当前节点与子节点比较之前，应该先比较两个子节点。如果是大顶堆，则选出更大的节点来与父节点比较，小顶堆则选出两者中更小的节点。

  3. 在比较两子节点时，也要注意子节点索引不能越界。同样在只有两个元素时进行 sink 操作的情况下，只有一个子节点，试图寻找此子节点的下一个子节点将会超越数组边界。例子：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    private void sink(int k) {
        int j = 2 * k;
        while (j <= N) {
            if (j+1 <= N && less((j + 1), j)) {
                j++;
            }
            if (less(j, k)) {
                exch(j, k);
                k = j;
                j *= 2;
            } else {
                break;
            }
        }
    }